Обучение математике маленьких детей – прямой путь к развитию их мышления, умения логически мыслить, сравнивать, выстраивать пространственные отношения, оперировать абстрактными категориями. И если для сторонников раннего развития это несомненный плюс и довод в пользу раннего обучения математики, то для многих психологов и родителей – это существенный минус. Давно установлено, что развитие абстрактного мышления происходит у человека в довольно позднем возрасте и его неоправданное стимулирование приводит к дисгармоничному формированию мозга и различным психологическим нарушениям. Усиленное развитие логики, большой объем абстрактных знаний и умений приводит к росту левого полушария мозга и задержке развития правого полушария, которое является доминирующим в раннем детстве. Поэтому, выбирая методику для обучения ребенка математике, постарайтесь не переусердствовать.
Великий психолог Жан Пиаже, исследуя, как дети образуют математические понятия, пришел к парадоксальному выводу: «Это большая ошибка – думать, что ребенок приобретает понятие числа и другие математические понятия непосредственно в обучении. Наоборот, в значительной степени он развивает их самостоятельно, независимо и спонтанно. Когда взрослые пытаются навязать ребенку математические понятия преждевременно, он выучивает их только словесно; настоящее понимание приходит только с его умственным ростом».
…Вместе с Гленном Доманом
Немного теории
В основе метода обучения математике, разработанного Гленном Доманом, лежит его убеждение в том, что учить ребенка необходимо в период роста его мозга, то есть с рождения и до 7-7,5 года. Учить его надо всему, в том числе математике. И делать это с помощью многочисленных карточек. Приготовьте плотный белый картон, самоклеящиеся красные кружочки диаметром 1,8 см и красный фломастер с толстым стержнем. Разрежьте картон на 100 квадратов размером 27,5×27,5 см. Сделайте комплект карточек с красными кружочками на каждой из них, от 1 до 100. Легче начинать с самой сложной карточки, со 100 кружочками, затем сделать карточку с 99 кружочками и т. д. Размещайте кружочки совершенно бессистемно, не наклеивайте их в виде треугольника, квадрата или какой-нибудь другой фигуры. Старайтесь, чтобы кружочки не касались и не перекрывали друг друга. У края карточки всегда оставляйте небольшие поля, чтобы ваши пальцы не закрывали кружочков. На обороте напишите карандашом количество кружочков.
Гленн Доман настоятельно рекомендует вести ежедневные записи, посвященные вашим занятиям с малышом. Во-первых, это хорошая памятка для вас, во-вторых, сопоставляя записи, вы сможете точно оценить достижения ребенка.
Родители, посещающие занятия в Институте Эвана Томаса, заполняют «Ежедневный контрольный листок». Возьмите и вы за правило вести подобный дневник.
Отмечайте следующее:
· частота занятий (чем и сколько раз вы сегодня займетесь с ребенком);
· интенсивность (как быстро малыш выполняет задание, сколько цифр или
математических действий он выучил);
· продолжительность (какое время отводится на выполнение каждого задания, общая продолжительность занятий за день);
· цель занятий (чего вы конкретно хотите достичь, выполняя упражнения. Например, запомнить цифру 3);
· замечания матери (добились ли вы поставленной цели, что не получается).
Практические упражнения
Гленн Доман считает, что обучение математике должно начинаться не с цифр, а с фактов. Поэтому нет смысла показывать малышу карточку с цифрой 8; необходимо показать ему карточку с восемью наклеенными кружочками. Ведь цифры – это всего лишь знаки, которые помогают представлять истинное количество. Гораздо проще сразу знакомить ребенка с этим количеством.
Этап 1 Узнаем количество
Первые пять карточек – это значение чисел от 1 до 5. Выберите момент, когда малыш пребывает в прекрасном расположении духа, сыт, здоров и не хочет спать. Покажите ему первую карточку с одним кружком и, улыбаясь, скажите: «Это один». Показывайте ему карточку только то время, что занимает произнесение фразы, затем эту карточку быстро уберите и покажите следующую, с двумя кружками. Скажите: «Это два». Затем продемонстрируйте карточки с числами 3, 4, 5. Не надо ничего объяснять ни словами, ни жестами, не надо заставлять ребенка повторять число. Просто четко произнесите число. После пятой карточки как-нибудь поощрите малыша (погладьте или поцелуйте). В течение дня повторите это занятие (с этими же числами) еще два раза. Итого три раза, примерно по минуте. Для первого дня достаточно. Интервал между занятиями произвольный, но не менее получаса. И не забывайте перетасовывать карточки, чтобы ребенок никогда не мог предсказать, какая карточка будет следующей. На следующий день ребенка ожидает шесть занятий. Три раза покажите пять вчерашних карточек и три раза набор из пяти новых, с цифрами от 6 до 10. И не забудьте каждый раз хвалить его! На шестой день пришла пора изымать некоторые карточки. Начиная с этого дня, вы должны ежедневно добавлять две новые карточки, а две старые изымать (на время). Так, в шестой день вы убираете карточки с числами 1 и 2, а добавляете карточки с числами 11 и 12. Получается, что вы каждый день проводите шесть уроков математики, каждый из них продолжается не более 10 секунд: по три раза демонстрируете каждый комплект, называя соответствующее карточке число. Каждый день вы изымаете по две старые карточки и добавляете новые. Так вы доходите до карточки с числом 100. Изучать числа дальше нет особого смысла, так как начинается, в основном, игра с нолями.
Этап 2 Изучаем равенства
Когда ребенок выучил числа от 1 до 20, переходите к следующему этапу – изучению равенств. Именно в это время он готов к тому, чтобы складывать некоторые количества вместе, то есть он готов приступить к сложению. Фактически, каждый день вы исподволь приучали его складывать числа, добавляя к предыдущему числу один кружочек. В течение нескольких недель вы будете чередовать занятия по изучению чисел и занятия с равенствами. Ваша ежедневная программа должна включать шесть занятий с числами и три занятия с равенствами. На обратной стороне каждой карточки заранее напишите равенства, например на карточке с числом 7: 1+ 6 = 7, 2 + 5 = 7, 3 + 4 = 7. Весело скажите: «Один плюс шесть равно семь», и покажите карточки с соответствующими числами. Это нужно сделать очень быстро – малышу совсем неинтересно следить, как вы перебираете карточки в поисках нужных. Поэтому все следует подготовить заранее и положить в нужной последовательности. Будьте последовательны, называя равенства, употребляйте одни и те же слова: плюс, равно (или равняется, или получится – но выберите только одно слова). Когда ребенок выучит факты, он сам установит правила. Каждый урок должен содержать не более трех равенств – можно меньше, но не больше. В день проводите по три занятия, причем на каждом предлагайте малышу три разных равенства и избегайте предсказуемости. Не следует на одном занятии показывать: 1+ 2 =3, 1+ 4 = 5, 1+ 5 = 6. Лучше покажите: 1+ 2 = 3, 2 + 5=7, 4 + 8 =12 Существует 190 различных равенств, которые можно составить с карточками от 1 до 20 Через две недели занятий необходимо перейти от сложения к вычитанию, иначе ребенок утратит интерес. Техника здесь аналогична. Громко и весело говорите: «Три минус два равно один» и показываете ребенку соответствующие карточки. Можно использовать карточки с числами больше 20, так как они уже знакомы ребенку. Занимайтесь вычитанием в течение двух недель, а затем переходите к умножению. Методика изучения равенств с умножением строится по тому же принципу, что сложение и вычитание. Скажите: «Два умножить на три равно шесть», и покажите карточки с нужными числами. Особо следует сказать о пустой карточке без всяких кружочков, которая обозначает «ноль». Вы должны ввести эту карточку в самом конце, когда изучили все числа от 1 до 100. Использовать ее нужно в равенствах, например: 6 + 0 = 6, 8 – 0 = 8, 12 x 0 = 0. Обычно дети обожают эту пустую карточку, обозначающую отсутствие всякого числа. Через две недели изучения умножения перейдите к делению и действуйте по тому же принципу. Громко произносите равенство: «Восемь разделить на четыре равно два», и показывайте карточки с числами. После двух недель занятий делением переходите к следующему этапу.
Этап 3 Решаем примеры
Для начала просто покажите ребенку две карточки, например 15 и 32. Спросите его, где 32. Если он смотрит на карточку с 32 кружочками или дотрагивается до нее – все прекрасно. Если нет – ничего страшного, возьмите нужную карточку и поднесите ему со словами: «Вот 32, не правда ли?» Выбор из двух карточек – хорошая тренировка перед тем, как перейти к решению примеров. В отличие от предыдущего этапа, вам надо будет показывать не три или больше карточек, а только две, и ребенок должен будет выбирать из них нужную. Скажите: «Двадцать два разделить на два равно одиннадцать», и покажите ребенку две карточки: 11 и, например, 27. Подождите, пока он выберет нужную, а если этого не случится – подскажите ему. Затем переходите к трехступенчатым примерам: 2×2x12 =? (48). Ежедневно вы должны показывать ребенку девять трехступенчатых равенств и один пример. После нескольких недель обучения таким равенствам усложните задание, введя в один пример два различных арифметических действия: 3 x 15-5 = 40 или 50 – 30 :10 = 2. Еще через две недели введите четырехступенчатые равенства. Если вы вдохновлены успехами вашего малыша и желаете продолжать обучение математике дальше, то с помощью предложенной методики займитесь:
· последовательностями (возрастающая: 5, 10, 15, 20, 25…; убывающая: 72, 70, 68, 66,64…; сложная: 6, 12, 10, 16, 14…);·
больше и меньше (сделайте карточки со значками < и > и показывайте в сочетании с различными числовыми карточками);·
равенствами и неравенствами (сделайте карточки со значками, обозначающими арифметические действия: +, -, х, = и др., выкладывайте их на полу в сочетании с различными числовыми карточками);
· особенностями чисел (сгруппируйте карточки по какому-нибудь признаку. Например: 12, 2, 3, 4, 6 или 60, 12, 15, 30, 30);
· дробями (говорите: «Одна третья от трех равно один», и покажите карточки 3 и 1);
· простой алгеброй (сделайте карточку со знаком у и показывайте ребенку уравнения,
например: 5 – у = 7, положите соответствующие карточки и равенство у = 2, а в следующий раз дайте ребенку возможность самостоятельно выбрать ответ).
Этап 4 Изучаем равенства с цифрами
Этот этап – повторение пройденного. Вам потребуются карточки размером 45×10 см, на которых вы напишете черным маркером равенства, примеры и уравнения. Первые карточки должны быть с ответами: 25 + 5 = 30, а затем без ответов: 25 + 5. Количество их неограниченно Занимайтесь математикой ежедневно по девять уроков в день.
Геометрия
Тема: «Тела вращения».
Занятие шестое. ЦИЛИНДР
 Вспомните, чем вы занимались на предыдущем занятии. Как называются шар и конус? (Тела вращения.) Какие у них общие свойства? Какие различия?
Вспомните, чем вы занимались на предыдущем занятии. Как называются шар и конус? (Тела вращения.) Какие у них общие свойства? Какие различия?
На геометрической льдине Ластик и Скрепочка познакомились еще с одним пингвиненком. Его звали Томми.
Покажите детям бумажную куклу-пингвиненка. Фрак Томми цилиндрической формы. Спросите детей: похожи ли Томми и Лолли? Что в них общего? Чем они отличаются?
Действительно, фрак ученого Томми другой формы. Эта форма называется цилиндром.
Достаньте модели конуса и цилиндра. Попросите детей сравнить фигуры.
Проведите опыт
Можно ли сделать несколько шагов с цилиндром и конусом на голове? А если перевернуть фигуры вверх ногами?
Сделайте вывод: у конуса одно основание, а у цилиндра — два. Основания обеих фигур имеют форму круга.
Спросите, что общего у цилиндра и у шара.
Вспомните про круг, «спрятанный» внутри шара.
В мешочках, лежащих на столах, дети должны нащупать цилиндр. (Кроме цилиндра, там находятся шар и конус.) Цилиндр надо достать.
Тактильное знакомство с фигурой
Провести ладонью по основаниям и боковой поверхности цилиндра.
Сделать то же с закрытыми глазами, повторяя: «Это цилиндр. У него два основания, боковая поверхность».
В переводе с греческого языка слово «цилиндр» означает «валик». Могут ли дети объяснить, почему?
Какие предметы в жизни напоминают цилиндр? (Валик маляра, каток трактора, труба водокачки или заводская труба, столбы и т.п.)
Проведите эстафету
Формируются три команды в составе 3—4 человек.
По сигналу играющие выбирают из разложенных на полу карточек рисунки с предметами шарообразной, конусообразной и цилиндрической формы. Выигрывает та команда, которая выберет нужные карточки без ошибок и быстрее всех.
Практическая работа
1. Слепить из пластилина цилиндр. Обмакивая одно основание в красную краску, а другое — в синюю, проложить цветную дорожку на белом листе — «льдине».
2. Используя пластилин, построить башню из цилиндра и конуса. Из башен можно составить целый город.
Занятие седьмое. РАЗВЕРТКИ ЦИЛИНДРА И КОНУСА
Покажите детям бумажных кукол — персонажей сказки. Пусть они вспомнят их имена, скажут, какую геометрическую форму имеет их одежда, опишут пирамиду, конус, цилиндр.
Как называются шар и конус? (Тела вращения.) Какие у них общие свойства? Какие различия?
Игра на различение фигур
Каждой фигуре соответствует определенное количество хлопков: шару — 0 (нет основания), конусу — 1 (одно основание), цилиндру — 2 (два основания), пирамиде — 3 (наименьшее количество вершин в основании пирамиды — 3).
У детей на столах — наборы из 4 фигур (из конструктора, счетного материала или самодельного). У педагога — набор демонстрационных фигур.
Первый вариант: педагог показывает фигуру, дети хлопают нужное количество раз.
Второй вариант: педагог называет фигуру, дети хлопают нужное количество раз.
Третий вариант: педагог хлопает определенное количество раз, дети показывают нужную фигуру.
Проведите опыт
Предложите двум желающим пройти с цилиндром на голове. В каком положении цилиндр почти невозможно удержать? В опытах с какими фигурами мы уже сталкивались с похожими ситуациями?
(В опытах с шаром и конусом, лежащим на боку.)
Предложите детям заставить фигуры катиться. Чем отличаются пути их движения? (Конус вращается вокруг своей вершины. Цилиндр может катиться либо вперед, либо назад. Шар катится в любом направлении.)
Сделайте вывод: Цилиндр — тоже фигура, способная вращаться. Шар, конус и цилиндр — тела вращения.
Пингвины с геометрической льдины в Антарктиде научили Ластика и Скрепочку одному чудесному превращению — плоских фигур в объемные. Покажите детям развертки поверхностей цилиндра и конуса. Развертки — это «развернутые» модели фигур.
Какая часть развертки послужит боковой поверхностью? Какая основанием? Покажите, как можно из разверток склеить объемные фигуры. Сделайте два цилиндра. Один из них снова разрежьте, чтобы получить развертку.
Спросите детей, можно ли подобным образом «развернуть» шар.
Проведите опыт со старым резиновым мячиком.
Шар нельзя развернуть в плоскую фигуру.
Точно так же нельзя развернуть глобус — модель Земли. А хорошо бы: носить глобус в рюкзаке во время путешествий не очень удобно. Лучше было бы положить туда что-нибудь плоское. Плоское изображение Земли назвали картой. Но при изготовлении карт возникли серьезные сложности. На карте Земля, как ни старайся, получается искаженной.
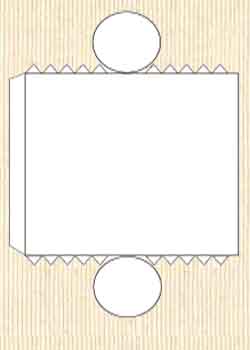
Практическая работа
У детей на столах развертки цилиндров. Надо рассмотреть развертки. Закрасить те части, которые соответствуют основаниям цилиндра, красным цветом, а те, которые являются боковой поверхностью фигур, — синим. Склеить развертки. Превратить их в веселых клоунов.
Занятие восьмое. КОНСТРУИРОВАНИЕ С ИСПОЛЬЗОВАНИЕМ РАЗВЕРТОК ЦИЛИНДРА И КОНУСА
Это заключительное занятие блока, посвященного телам вращения.
Спросите детей: в какие края отправились Ластик и Скрепочка и с кем они там познакомились?
Попросите детей найти Антарктиду на глобусе и вспомнить все, что они знают об этом материке. Расскажите, что в Антарктиде очень холодно и снег никогда не стаивает. Земля промерзла так глубоко, что ни деревья, ни кусты там не растут. Люди в Антарктиде не живут: там нет ни городов, ни деревень. Только ученые-полярники отправляются в антарктические экспедиции. Но и в этом суровом краю обитают животные и птицы.
Путешествуя по Антарктиде, Ластик и Скрепочка узнали, что пингвины не умеют летать, зато они очень хорошо плавают.
Ластик и Скрепочка наблюдали, как пингвины бросались в ледяную воду за добычей и вдруг быстро выпрыгивали обратно: это на них нападал их злейший враг — морской леопард.
А еще они познакомились с другими жителями Антарктиды. Это большекрылые птицы альбатросы и неуклюжие тюлени.
Предложите детям выбрать себе развертки, из которых они смогут смастерить обитателей Антарктиды. Спросите, какие фигуры угадываются в развертках. Создайте коллективный макет «Ластик и Скрепочка в гостях на геометрической льдине».
Ольга БАРАНОВА,
лауреат конкурса «Учитель года России-97»,
г. Барнаул
Вырежьте детали заготовки. Согните деталь 1 и склейте из нее цилиндр — фрак Томми. Отогните клапаны внутрь цилиндра и приклейте к ним донышки (детали 2 и 3). Приклейте к нему крылышки 4 и 5, как показано на рисунке на с. 13. Клюв (деталь 8) согните по пунктирным линиям и приклейте. Лапки пингвина (детали 6 и 7) приклейте к донышку. Томми готов.
|
|
|
| ||
| ||
Игры со счетными палочками Кюизинера и блоками Дьенеша
Условные обозначения для блоков Дьенеша